´

Original research

 

Design and validation of a short-implant rehabilitation model

Design e validação de um modelo dreabilitação com implantes curtos

 

José Joaquim da Rocha Ferreira^a,b,*, José Manuel Oliveira^b, Santiago D. Castellanos^b, André Correia^c,d, Ana Rosanete Reis^a,b

^a Faculdade de Engenharia da Universidade do Porto (FEUP)/ Instituto de Engenharia Mecânica e Gestão Industrial (INEGI), Porto, Portugal

^b Instituto de Engenharia Mecânica e Gestão Industrial (INEGI), Porto, Portugal

^c Universidade Católica Portuguesa, Instituto de Ciências da Saúde, Viseu, Portugal

^d Universidade Católica Portuguesa, CIIS – Centro de Investigação Interdisciplinar em Saúde, Instituto de Ciências da Saúde, Viseu, Portugal

 

^*Correspondence to:

 

http://doi.org/10.24873/j.rpemd.2017.07.017

 

Abstract

Objectives: This research intended to develop and validate a digital model that could be used to study the stresses and strains created in the different components involved in oral fixed rehabilitations with short implants. The validated model was then used to simulate a clinical-like situation.

Methods: A digital model was created considering the posterior areas of the mandible. Its materialization obtained ten specimens of the experimental prototype. Seven of them were static compressive tested until failure and, for the other three, the tests were progressively interrupted, to allow the establishment of a damage sequence. On the numerical model a finite element analysis was performed with Abaqus software, under similar conditions to the experimental situation.

Results: The stress pattern on the FEA and the failure location on the static test were similar. The sequence in which each part reached the yield strength was the same as that observed on the interrupted static test (resin, prosthetic framework, implants and implant screws, in this order). Due to these results, the model was considered valid. A clinical-like simulation with the validated model showed that buccal cortical bone, around the implants platform, is the weakest part of such a rehabilitation.

Conclusions: This research allowed the development and validation of a computer-aided design model that can be used to study an oral fixed rehabilitation supported by short implants. For clinical purposes, it is important to refer that the highest stress and strain values were found on the cortical bone around the buccal aspect of the implants. (Rev Port Estomatol Med Dent Cir Maxilofac. 2017;58(2):79-90).

Keywords: Experimental model, Numerical model, Short implants, Stress and strain

 

Resumo

Objetivos: O objetivo desta investigação foi o desenvolvimento e validação experimental de um modelo digital, que permita o estudo das tensões e deformações geradas nos diferentes componentes de uma reabilitação oral fixa sobre implantes curtos. O modelo obtido foi então usado para simular uma situação clinica.

Métodos: Um modelo numérico foi criado considerando a regiao posterior da mandíbula. A sua materialização permitiu obter dez amostras do protótipo experimental. Sete delas foram sujeitas a ensaios estáticos de compressão até a falência. Nas restantes tres, os ensaios foram interrompidos com forcas gradualmente crescentes, estabelecendo a sequencia pela qual os componentes se deformaram. O modelo numérico foi também sujeito a uma simulação com elementos finitos, usando o software Abaqus, em condições semelhantes a simulação experimental.

Resultados: O padrão de tensões obtido no modelo numérico foi similar a localização das fraturas no modelo experimental. A sequencia segundo a qual a tensão de cedência foi alcançada em cada parte do modelo numerico foi a mesma encontrada quando o ensaio estático se interrompeu (por esta ordem: resina, prótese, implantes e parafusos). Estes resultados permitiram considerar o modelo valido. A simulação de uma situação clinica, com o modelo validado, revelou que o osso cortical, em vestibular da plataforma dos implantes, e a região mais débil da reabilitação.

Conclusões: Esta investigação permitiu o desenvolvimento e a validação de um modelo que permite o estudo de reabilitações fixas sobre implantes curtos. Clinicamente e importante realcar que o osso cortical e a zona que apresenta tensões e deformações mais elevadas. (Rev Port Estomatol Med Dent Cir Maxilofac. 2017;58(2):79-90).

Palavras-chave: Modelo experimental, Modelo numérico, Implantes curtos, Tensao e deformacao

 

Introduction

Short dental implants are considered a viable option for supporting a fixed oral rehabilitation on the posterior mandible regions with advanced crestal bone resorption.1 This solution represents an alternative to more invasive surgeries such as bone grafting, guided bone regeneration, distraction osteogenesis or lateralization of the alveolar nerve.^2,3 The definition of short implants is still non‑consensual among authors.

Some consider a short implant when its length is shorter than 10 mm,^1,4,5 while other authors propose 8 mm as the maximal length to define a short implant.^6,9 Some studies, comparing these implants regarding parameters such as survival rates, marginal bone loss or prosthetic complications, did not found statistically significant differences.^1,10-14 However, consideration should be given to the fact that the studies involving these implants, due to their relatively recent clinical introduction, are not long‑term studies As result of their clinical applications and success rates, the use of short implants is increasing significantly.¹

The biomechanical rational for the use of these implants relies on the finding that after the first 7 mm only a reduced stress can be measured on the implant surface,11 and, to support the masticatory load, the cervical portion of the implant is the most involved.¹⁵ In agreement with these findings it was also reported that bone stress is independent of the implant’s length.¹⁶

The use of rough surfaces, by increasing the implant‑bone contact area, has also been documented as having a positive impact on the biomechanical performance of short implants.^4,17,18

Likewise, the choice for an internal connection with the platform shifting concept seems to promote a better sealing and less micromovements, promoting the preservation of the bone crest level.^19-21

However, if the safety of use seems to be well established, some concerns and controversial results still exist. In opposition to the studies that reported low marginal bone loss, Tabrizi et al²² showed that the fewer the number of short implants supporting a fixed prostheses, the greater the marginal bone loss found. Likewise, Bhat et al²³ on a finite element analysis (FEA), found that the maximum Von Mises equivalent stress was measured on the cortical bone, and that it increased in both cortical and cancellous bone when the implant length decreased. A similar behaviour was found by Himmlova et al.²⁴

Although not considered statistically significant, the resonance frequency analysis performed by Calvo‑Guirado et al²⁵ showed that the ISQ values for short implants were lower than those found for longer implants. Nisand et al,³ explained the possible failure of short implants with a reduced implant primary stability, bone‑to‑implant contact, as well as an unfa-vourable crown‑to‑implant ratio. Biomechanical studies highlight the danger represented by the bending loads either for short implants, once they have a smaller area to dissipate tensions,^2,26 or for cortical bone because its yield strength is lower when the load is acting on a perpendicular direction to its major axis.²⁷ In a location where higher masticatory loads are produced, as the posterior arch, these findings are of utmost importance. A study from Malmstrom et al²⁸ considered the compromised crown‑to‑implant ratio and the lower bone‑to‑implant contact area, factors of more concern when the masticatory loads are higher or when the patient presents risk factors for periimplantites.

Due to all these variables, some authors still include the implants length on the list of risk factors for implant failure.^29-31

As biomechanical methods were suggested to decrease the stress found on the biologic structures,³² FEA may be beneficial for the comprehension of the mechanical behaviour of all the parts involved in such a rehabilitation. This in silico approach has been widely used on dental implant research, allowing multiple combinations of critical factors in a short period of time.³³ However, it´s accuracy is extremely dependent on factors such as the model geometry, simplifications, material properties, boundary conditions, applied load, type of mesh and contact definitions.^24,33 The more the virtual model resembles reality, the more accurate the results will be and, to rely on the FEA results, an experimental validation is required.³⁴

It must be noted that, due to those differences, an absolute coincidence in the magnitudes of loads, stresses and strains is not the objective. The propose is to obtain on both, numerical analysis and mechanical experiment, the same behaviour and tendency.^35,36

The aim of this research was the development and experimental validation of a numerical model that could be used in the study of stresses and strains created in the different components involved in oral fixed rehabilitations with short implants.

Material and methods

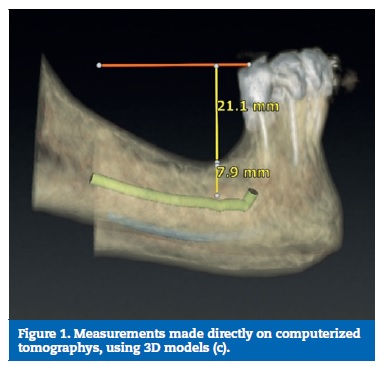
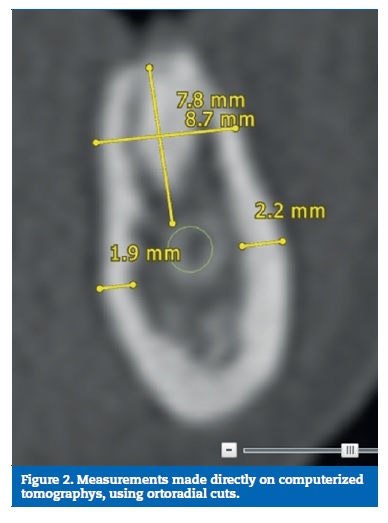
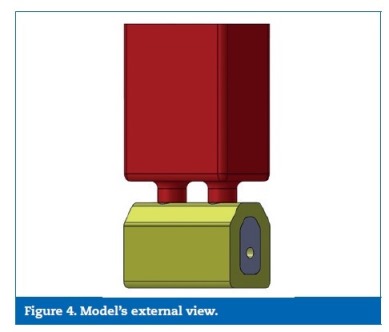
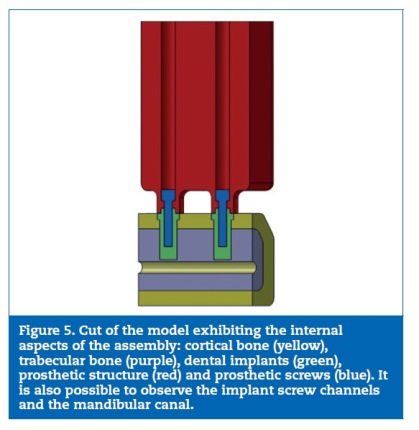
A digital model considering the posterior areas of the mandible was designed with SolidWorksR software (Dassault Systemes SA, Velizy, France). The dimensions were obtained considering the mean of ten direct measurements on patients’ computerized tomographys, reverse engineering and product catalogues (Figures 1 to 3). Considering the obtained measurement for the overall model’s high (37 mm) and the clinical case that was intended to simulate (a mandible with a reduced bone volume but where the placement of short implants was possible), the obtained model resulted in an accentuated crown‑to‑implant disproportion, where the prosthetic framework (25 mm) is four times higher than the supporting implant (6 mm) (Figures 4 and 5). In order to test the worst‑case scenario, the use of external hexagon connection implants was preferred, based on the suggestion that this type of connection exhibits weaker biomechanical performance^19-21 than internal connections. The model was completed by the design of four parts: a type II bone, with a 2 mm cortical, regular platform implants, implant screws and prosthetic framework. To save calculation time the geometries were simplified.

The created model followed two different procedures: a) Design for manufacturing (DFM) and prototyping; b) FEA simulation performed with AbaqusR software (Dassault Systemes SA, Velizy, France).

 

 

 

 

 

 

 

 

 

 

 

 

 

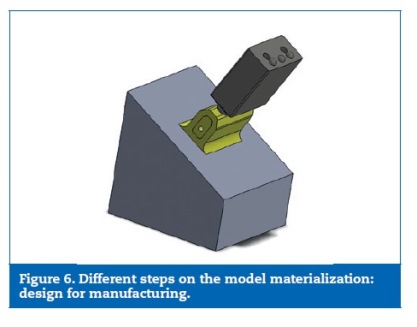
Regarding the former, for set up proposes, respecting the ISO standard 14801,³⁷ a base was coupled to the bone part to place the samples on the machine test with an angulation of 30^o with the vertical. The DFM also comprehended the introduction of tolerances on the prosthetic framework and the modelling of three semi‑spheres for the load appliance (Figure 6).

 

 

 

On the prototype construction, the base and the bone part were made of epoxy resin. The framework was milled on a cobalt‑chrome alloy (DMU 60 eVe; DMG MORI, Tokyo, Japan) and screw retained with a tightening torque of 35 Ncm. The used implants were Nobel Speedy dummies, cut to 6 mm and the implant screws were manufactured on the same company (Nobel Biocare AB, Gothenburg, Sweden) (Figure 7). To obtain the resin part, a stereolithographic model was build (Figure 8). From this model resulted a silicon mould, where the framework with the implants was placed, and into which the resin was poured (Figure 9), to allow a perfect alignment of all components and ensure a correct replication for all samples (Figure 10).

 

 

 

 

 

 

 

 

Ten samples were constructed using the described methodology.

Seven of them were static tested until failure, on a uniaxial universal Instron test machine (Norwood, MA, USA), calibrated and suitable for the intended study. Once the results were similar to all specimens, three more samples were tested until 3000N, 4000N and 5000N, to establish the failure sequence of the different parts (Figure 11).

 

 

 

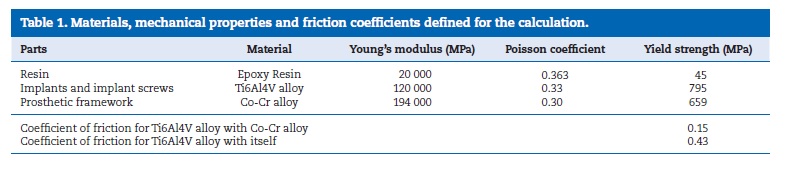
To perform the FEA it was necessary the equalization of both, virtual and experimental models. For that propose, the bone part was transformed into resin by merging cortical and trabecular bone and assigning to it the epoxy resin mechanical elastic characteristics. Those were obtained by the performance of static tensile load tests according with the standards ASTM D‑638‑02a³⁸ and ISO 527‑139 (Figure 12). The properties of implants, implant screws and prosthetic framework were obtained from bibliography and product catalogues^40-46(Table 1).

All the model parts were considered to be solid, homogeneous and isotropic. The resin and implants were merged to simulate an osteointegration‑like situation. Interactions and constraints were defined to approach the experimental situation.

 

 

 

 

 

Three circular areas for load appliance, correspondent to the described semi‑spheres, were defined⁴⁷. According to ISO standard 14801, the load was applied forming 30 degrees with the implant long axis. A magnitude of 3000 N per each area was chosen, in order to largely overcome the yield strength of all materials. This procedure allowed the analysis of the stresses for each force increment and register the sequence by which the materials reached their elastic limit.

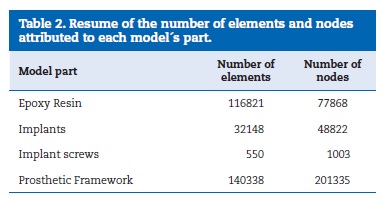
A mesh study was performed to obtain the stress convergence and to enable the mesh refinement where more accurate results where needed. A coarser mesh was defined elsewhere to save calculation time. The parts were meshed separately with quadratic tetrahedral elements (Table 2, Figure 13). A boundary condition was defined on the lower border of the resin to avoid displacements or rotations.

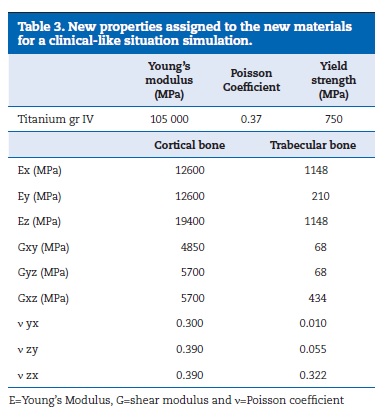
In case of verifying the model validation, a clinical approach could be performed by reassuming the bone part, with cortical and trabecular bone, changing the implants material properties to commercial pure grade IV titanium and applying a physiological load.⁴⁷ Because, contrary to the isotropy of resin, the bone shows orthotropic characteristics, properties would have to be defined taking into account the Cartesian coordinate system^48-50(Table 3). The model design and other sets were maintained.

 

 

 

 

 

 

 

Results

On this study two aspects were analysed: a) the location of the higher stresses on FEA in comparison with the material failures on the experimental model; b) the damage sequence on the experimental model in comparison with the yield strength reaching sequence at FEA.

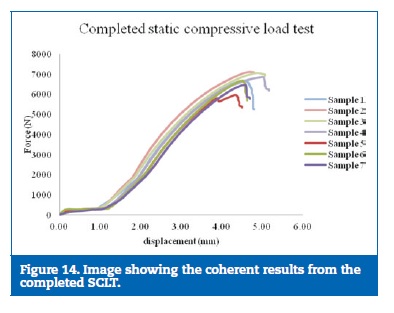
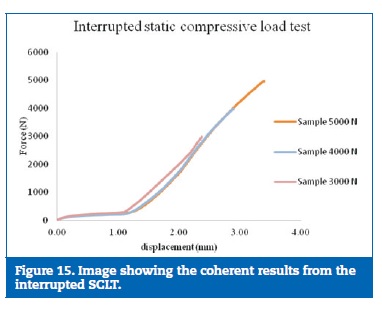
The results on the static test were considered consistent due to the reproduction of the force‑displacement curve on all the samples tested (Figures 14 and 15).

 

 

 

 

 

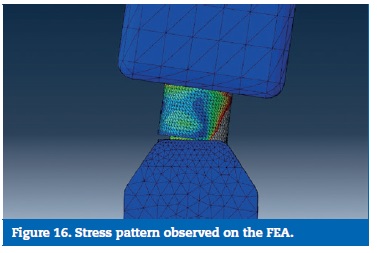
For each model part, the FEA higher stresses locations were identified and compared to the location where, on the experimental model, the material failed. As so, it was possible to list the following events:

As result of the load direction, a bending moment was created, leading to a rotational displacement on the virtual and the experimental model. The framework connectors suffered a compression on their buccal aspect, with the highest stresses found on that location, while an open joint was observed on the lingual aspect. This behaviour was found on both models (Figures 16 and 17).

The implants revealed the higher stresses on the buccal aspect of the platform. Following the same tendency, the experimental model exhibited implant fractures on the corresponding sites.

The resin showed the highest stresses buccally to the implant platform. The compressive tests also resulted in resin fracture at the same location.

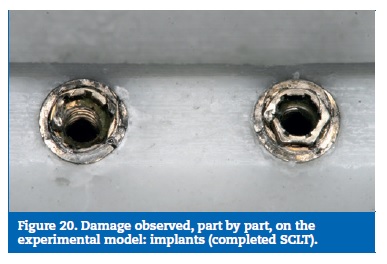
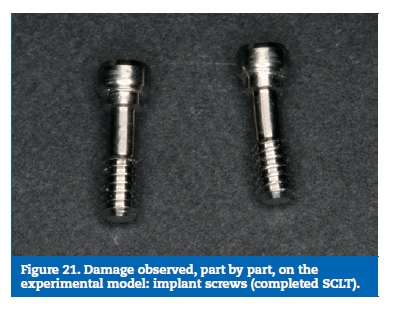
Finally, the implant screws higher stresses were found at the lingual aspect of the screw body, as result of the bending solicitations. On the experimental model, two screws were found deformed with the same trend and the others did not reach plastic deformation (Figures 18 to 21).

 

 

 

 

 

 

 

 

 

 

 

 

 

To compare the sequence of events on both models, the interrupted static load tests results where compared with the step increment in which, each part, reached the yield strength on the FEA.

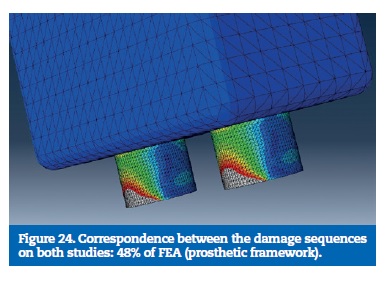
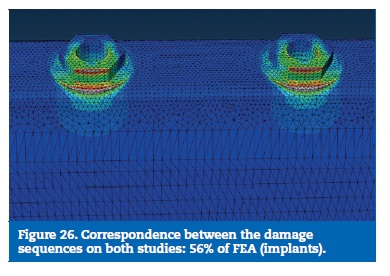
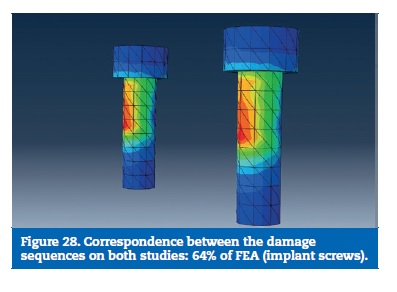
The static load tests, interrupted in a sequence of progressive higher loads, contributed to clarifying the damage sequence on the experimental model. With 3000N only the resin suffered small fractures. With 4000N was possible to observe an initial deformation of the prosthetic framework connectors, more evident at 5000N. The implants and the implant screws did not show any plastic deformation for these loads. Based on the results obtained on both, interrupted and completed static tests, it was possible to determine the sequence in which the model parts are affected: First is the resin, second is the prosthetic framework, third the implants and the implant screws are the most resistant part.

On the FEA model, the resin reached the calculated yield strength with 16% of the load. With 48% of the applied load, the stress on the prosthetic framework connectors overcame the elastic limit. The implants reached the plastic deformation zone for a 56% of the total load and the implant screws were the last part to reach the yield strength (Figures 22 to 29).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

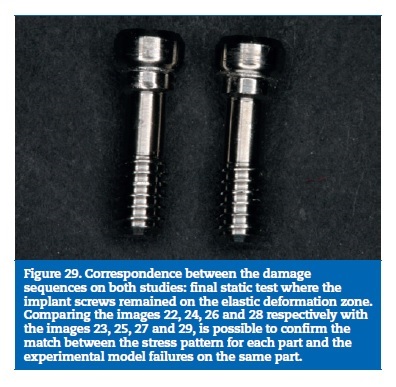
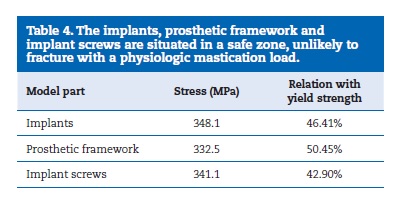
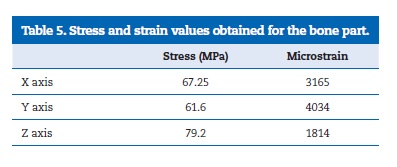
The results of the simulation of a clinical scenario are depicted on the Tables 4 and 5. Table 4 shows the results of the metallic components, comparing the measured stress with the yield strength of each material. The stresses found on the different components are very similar, reaching around 50% or less of the yield strength. Table 5 shows the results of the bone part, considered as an orthotropic material, highlighting the stresses and microstrains obtained for each Cartesian coordinate.

The higher value for stress was found on the Z axis while the higher microstrain was found on the Y axis.

 

 

 

 

 

Discussion

Analysing the tendencies of both models is possible to observe an absolute match of their biomechanical behaviours.

The stress pattern measured on the FEA was confirmed with the failure location on the SCLT and the sequence in which each part reached the yield strength was the same as the observed on the interrupted SCLT. As Kim et al35 and Eser et al³⁶ have demonstrated, a coincidence of tendencies and behaviours is the condition needed to validate a numerical model, once all the simplifications and assumptions made during the numerical modelling impair a quantitative coincidence of the results. So, because the results show the necessary coincidence of behaviours, the model was considered valid to study the biomechanical behavior of an implant‑fixed oral rehabilitation with recourse to short implants.

The calculation performed using the validated model, simulating a clinical situation, indicated that the metal parts of the model are in a very safe zone, away from the plastic deformation. The interpretation of the results on the bone part is, due to its orthotropy, more complex. As the Von Mises equivalent stress express the six components of stress in only one value, it is very difficult to be compared with an anisotropic material’s yield strength. The values of 182 MPa and 121 MPa for the yield strength, considering, respectively, a compression load parallel or normal to the bone major axis, were suggested by Natali et al.⁵¹ However, the Frost’s mechanostatic theory,⁵² without referring to the orthotropic variations, indicated that, for a stress of 60 MPa and a strain of 3000 microstrain, the bone’s yield point would be achieved resulting in woven bone rather than lamellar formation. Likewise, Carter’s hypothesis^13,53sustain that a bone strain over 4000 microstrain can cause bone loss.

It is possible to observe that the microstrain measured on the X and Y axis, as well as the stress measured on the Z axis, are on a dangerous zone with a very high possibility of bone overloading and bone loss.

These results highlight the fact that bone is the weakest part of such a rehabilitation, especially the buccal cortical bone, around the implants platform. This finding is of extreme importance once it may result in bone resorption, initiating a sequence of events that may result in implant failure. It is also extremely important because bone, the only biological tissue considered in this experiment, is also the most difficult part to replace.

Tabrizi et al,²² Bhat et al²³ and Himmlova et al,²⁴ share the same concerns related with the cortical bone preservation around short implants platform. On contrary, analysing unsplinted short‑implant rehabilitations, Nissan et al⁵⁴ found prosthetic failures for a crown‑to‑implant ratio of 1,75‑1.

To decrease the stress and strain observed at the cortical bone level, the intervention at the prosthetic framework geometry could represent a valid alternative. It is worth remember that the presupposition of this study was to avoid complex surgical techniques to augment the available bone volume.

Conclusions

This research allowed the development and validation of a computer‑aided design model that can be used to study an oral fixed rehabilitation supported by short implants.

The highest stress and strain values were found on the cortical bone around the buccal aspect of the implants.

Future research should focus on modifying the geometry of the prosthetic framework in order to promote a decrease of stress and strain on cortical bone, contributing to avoid bone resorption and implant loss.

 

References

¹. Pommer B, Busenlechner D, Furhauser R, Watzek G, Mailath‑Pokorny G, Haas R. Trends in techniques to avoid bone augmentation surgery: Application of short implants, narrow‑diameter implants and guided surgery. Journal of Cranio‑Maxillofacial Surgery. 2016.

². Pellizzer EP, de Mello CC, Santiago Junior JF, de Souza Batista VE, de Faria Almeida DA, Verri FR. Analysis of the biomechanical behavior of short implants: The photo‑elasticity method. Materials Science and Engineering: C. 2015;55:187‑92.

³. Nisand D, Renouard F. Short implant in limited bone volume. Periodontology 2000. 2014;66:72‑96.

⁴. Mezzomo LA, Miller R, Triches D, Alonso F, RSA. S. Meta‑analysis of single crowns supported by short (<10 mm) implants in the posterior region. J Clin Periodontol. 2014;41:191-213.

⁵. Fugazzotto P. Shorter implants in clinical practice: rationale and treatment results. International Journal of Oral and Maxillofacial Implants. 2008;23:487‑96.

⁶. Renouard F, Nisand D. Impact of implant length and diameter on survival rates. Clin Oral Implan Res. 2006;17:35‑51.

⁷. Esposito M, Felice P, Worthington HV. Interventions for replacing missing teeth: augmentation procedures of the maxillary sinus. Cochrane Database of Systematic Reviews. 2014.

⁸. Sung‑Ah L, Chun‑The L, Martin M F, Waeil E, Sung‑ Kiang C. Systematic Review and Meta‑Analysis of Randomized Controlled Trials for the Management of Limited Vertical Height in the Posterior Region: Short Implants (5 to 8 mm) vs Longer Implants (> 8 mm) in Vertically Augmented Sites. International Journal of Oral & Maxillofacial Implants. 2014;29:1085-97.

⁹. Fugazzotto P, Beagle J, Ganeles J, Jaffin R, Vlassis J, Kumar A. Success and failure rates of 9 mm or shorter implants in the replacement of missing maxillary molars when restored with individual crowns: preliminary results 0 to 84 months in function. A retrospective study. J Periodontol. 2004;75:327‑32.

¹⁰. Lemos CAA, Ferro‑Alves ML, Okamoto R, Mendonca MR, Pellizzer EP. Short dental implants versus standard dental implants placed in the posterior jaws: A systematic review and meta‑analysis. Journal of dentistry. 2016;47:8‑17.

¹¹. Renouard F, Rangert B. Treatment Sequence and Planning Protocol. Risk Factors in Implant Dentistry Simplified Clinical Analysis for Predictable Treatment. 2nd ed. Chicagi: Quintessence books; 2008;146‑50.

¹². Renouard F, Nisand D. Impact of implant length and diameter on survival rates. Clinical Oral Implants Research. 2006;17(S2):35‑51.

¹³. Mendoza‑Azpur G, Lau M, Valdivia E, Rojas J, Munoz H, Nevins M. Assessment of Marginal Peri‑implant Bone‑Level Short‑Length Implants Compared with Standard Implants Supporting Single Crowns in a Controlled Clinical Trial: 12‑Month Follow‑up. The International journal of periodontics & restorative dentistry. 2016;36:791.

¹⁴. Camps‑Font O, Burgueno‑ Barris G, Figueiredo R, Jung RE, Gay‑Escoda C, Valmaseda‑Castellon E. Interventions for Dental Implant Placement in Atrophic Edentulous Mandibles: Vertical Bone Augmentation and Alternative Treatments. A Meta‑Analysis of Randomized Clinical Trials. Journal of Periodontology. 2016;1‑23.

¹⁵. Kim S, Kim S, Choi H, Woo D, Park Y‑B, Shim J‑S, et al. A three‑dimensional finite element analysis of short dental implants in the posterior maxilla. International Journal of Oral & Maxillofacial Implants. 2014;29:155‑64.

¹⁶. Anitua E, Tapia R, Luzuriaga F, Orive G. Influence of implant length, diameter, and geometry on stress distribution: a finite element analysis. International Journal of Periodontics & Restorative Dentistry. 2010;30:89‑96.

¹⁷. Renouard F, Nisand D. Short Implants in the Severely Resorbed Maxilla: A 2‑Year Retrospective Clinical Study. Clin Implant Dent Relat Res. 2005;7:s104‑s10.

¹⁸. Deporter D, Watson P, Pharoah M, Todescan R, Tomlinson G. Ten‑Year Results of a Prospective Study Using Porous‑Surfaced Dental Implants and a Mandibular Overdenture. Clinical Iinplant Dentistry and Related Research. 2002;4:183‑9.

¹⁹. Yamanishi Y, Yamaguchi S, Imazato S, Nakano T, Yatani H. Influences of implant neck design and implant–abutment joint type on peri‑ implant bone stress and abutment micromovement: Three‑dimensional finite element analysis. Dent mater. 2012;28:1126‑33.

²⁰. Feitosa P, de Lima A, Silva‑Concilio L, Brandt W, Claro Neves A. Stability of external and internal implant connections after a fatigue test. Eur J Dent. 2013;7:267‑71.

²¹. Ferreira J, Franca M, Correia A, Reis A. Implant-abutment geometry and its role in bone level preservation. in: Natal Jorge R et al, editors. Proceedings of the Biodental Engineering II; 2012 Dec 7-8; Porto, Portugal: CRC Press. 2014;79-84

²². Tabrizi R, Arabion H, Aliabadi E, Hasanzadeh F. Does increasing the number of short implants reduce marginal bone loss in the posterior mandible? A prospective study. British Journal of Oral and Maxillofacial Surgery. 2016;54:731‑5.

²³. Bhat SV, Premkumar P, Shenoy KK. Stress Distribution Around Single Short Dental Implants: A Finite Element Study. The Journal of Indian Prosthodontic Society. 2014;14(1):161‑7.

²⁴. Himmlova L, Dostalova Tj, Kacovsky A, Konvickova S. Influence of implant length and diameter on stress distribution: A finite element analysis. The Journal of Prosthetic Dentistry. 2004;91:20‑5.

²⁵. Calvo‑Guirado JL, Lopez Torres JA, Dard M, Javed F, Perez‑Albacete Martinez C, Mate Sanchez de Val JE. Evaluation of extrashort 4‑mm implants in mandibular edentulous patients with reduced bone height in comparison with standard implants: a 12‑month results. Clinical Oral Implants Research. 2016;27:867‑74.

²⁶. Verri FR, Junior JFS, de Faria Almeida DA, de Oliveira GBB, de Souza Batista VE, Honorio HM, et al. Biomechanical influence of crown‑to‑implant ratio on stress distribution over internal hexagon short implant: 3‑D finite element analysis with statistical test. Journal of biomechanics. 2015;48:138‑45.

²⁷. Keaveny T, Morgan E, OC Y. Bone Mechanics. In: M. Kutz, editor. Standard Handbook of Biomedical Engineering and Design. New York: McGraw‑ Hill Professional; 2003.

²⁸. Malmstrom H, Gupta B, Ghanem A, Cacciato R, Ren Y, Romanos GE. Success rate of short dental implants supporting single crowns and fixed bridges. Clinical Oral Implants Research. 2016;27:1093‑8.

²⁹. Chrcanovic BR, Albrektsson T, Wennerberg A. Reasons for failures of oral implants. Journal of Oral Rehabilitation. 2014;41:443‑76.

³⁰. Olmedo‑Gaya MV, Manzano‑Moreno FJ, Canaveral‑Cavero E, de Dios Luna‑del Castillo J, Vallecillo‑Capilla M. Risk factors associated with early implant failure: A 5‑year retrospective clinical study. The Journal of prosthetic dentistry. 2016;115:150‑5.

³¹. Sennerby L, Gottlow J. Clinical outcomes of immediate/early loading of dental implants. A literature review of recent controlled prospective clinical studies. Australian dental journal. 2008;53(s1):S82‑S8.

³². Misch C. Short dental implants: a literature review and rationale for use. Dentistry today. 2005;24:64-66,68.

³³. Toro‐Ibacache V, Fitton LC, Fagan MJ, O’Higgins P. Validity and sensitivity of a human cranial finite element model: implications for comparative studies of biting performance. Journal of anatomy. 2016;228:70‑84.

³⁴. Groning F, Liu J, Fagan M, O’Higgins P. Validating a voxel‑based finite element model of a human mandible using digital speckle pattern interferometry. Journal of biomechanics. 2009;42:1224‑9.

³⁵. Kim H‑S, Park J‑Y, Kim N‑E, Shin Y‑S, Park J‑M, Chun Y‑S. Finite element modeling technique for predicting mechanical behaviors on mandible bone during mastication. J Advanc Prosthod. 2012;4:218‑26.

³⁶. Eser A, Akca K, Eckert S, Cehreli MC. Nonlinear finite element analysis versus ex vivo strain gauge measurements on immediately loaded implants. Int J Oral Maxillofac Impl. 2009;24:439‑46.

³⁷. International Standard Organization. 14801. Dentistry – Implants – Dynamic fatigue test for endosseous dental implants. Switzerland, 2007.

³⁸. American Society for Testing and Materials. D638‑ 02a. Standard test method for tensile properties of plastics. United States of America, 2003.

³⁹. International Standard Organization. 527‑1. Plastics – Determination of tensile properties – Part 1: General principles. Switzerland, 2012.

⁴⁰. MatWeb [Internet]. Material property data [cited 2 Nov 2016]; [about 1 screen]. Available from: http//www.matweb.com/search/Datasheet.aspx?matGUID=237df255c8324fe6a06dc004e86d86b6.

⁴¹. MatWeb [Internet]. Material property data [cited 2 Nov 2016];[about 1 screen]. Available from: http//www.matweb.com/search/Datasheet.aspx?MatGUID=b350a789eda946cc6b86a3e4d3c577b39.

⁴². NobelBiocare. Material characteristics. Product Catalog, Complete Assortment, 2011;350.

⁴³. Avinent. Informacion sobre estructuras fresadas en CrCo. In: Protech SLCD, editor. 2013.

⁴⁴. Fonseca E, Mendes C, Noronha J. Estudo comparativo da influencia de diferentes materiais em protese num fémur humano. Paper presented at: 8.^o congresso de mecânica experimental; 2010 Apr 21-23; Guimaraes, Portugal. Portuguese.

⁴⁵. Fessler H, Fricker D. Friction in Femoral Prosthesis and Photoelastic Model Cone Taper Joints. Proc Inst Mech Eng H.1989;203:1‑14.

⁴⁶. Budinski KG. Tribological properties of titanium alloys. Wear. 1991;151:203‑17.

⁴⁷. Baca E, Yengin E, Gokcen‑ Rohlig B, Sato S. In vivo evaluation of occlusalcontact area and maximum bite force in patients with various types of implant‑supported prostheses. Acta Odontol Scand. 2013;71:1181‑7.

⁴⁸. O’Mahony A M, Williams J L, Spencer P. Anisotropic elasticity of cortical and cancellous bone in the posterior mandible increases periimplant stress and strain under oblique loading. Clin Oral Impl Res. 2001;12:648-57.

⁴⁹. ASM Aerospace Specification metals inc. [Internet]. [Cited Nov 2015]; [about 1 screen].Available from: http://asm.matweb.com/search/SpecificMaterial.asp?bassnum=mtu040.

⁵⁰. NobelBiocare. Material characteristics. Product Catalog, Complete Assortment, 2011;356.

⁵¹. Natali AN, Hart RT, Pavan PG, Knets I. Mechanics of bone tissue. In: AN N, editor. Dental biomechanics: Taylor & Francis Inc. 2003;1‑19.

⁵². Frost HM. Bone’s Mechanostat: A 2003 Update. ANAT REC PART A. 2003;275A:1081‑101.

⁵³. Baggi L, Cappelloni I, Di Girolamo M, Maceri F, Vairo G. The influence of implant diameter and length on stress distribution of osseointegrated implants related to crestal bone geometry: A three‑dimensional finite element analysis. J Prosthet Dent. 2008;100:422‑31.

⁵⁴. Nissan J, Ghelfan O, Gross O, Priel I, Gross M, Chaushu G. The effect of crown/implant ratio and crown height space on stress distribution in unsplinted implant supporting restorations. J Oral Maxillofac Surg. 2011;69:1934‑9.

 

^*Corresponding author:

Jose Joaquim da Rocha Ferreira

E-mail address: jose.j.r.ferreira.299@gmail.com

 

Ethical disclosures

Protection of human and animal subjects. The authors declare that no experiments were performed on humans or animals for this study.

Confidentiality of data. The authors declare that no patient data appear in this article.

Right to privacy and informed consent. The authors declare that no patient data appear in this article.

 

Funding

The study was supported in part by SciTech - Science and Technology for Competitive and Sustainable Industries, and the R&D project was cofinanced by the North Portugal Regional Operational Program (“NORTE2020”) and the European Regional Development Fund (FEDER).

 

Conflicts of interest

The authors have no conflicts of interest to declare.

 

Acknowledgements

The authors gratefully acknowledge the INEGI, particularly to Mr. Jose Teixeira, Mrs. Andreia Duraes and Mr. Sertorio Lares, for their help on the specimens and experimental set up preparation.

 

Article history:

Received 14 December 2016

Accepted 28 June 2017

Available online7 July 2017